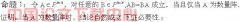在初三代数的函数及其图象中,蕴含的辩证观点极为丰富。这一章教学内容的最大特点是"变":变化、变量、运动,正如恩格斯所说的"数学中的转折点是笛卡儿的变数。有了变数,运动进入了数学,有了变数,辩证法进入了数学,有了变数,微分和积分也就立刻成为必要的了。"?
现代课程理论及教学实践证明,搞好这一章的教学,不仅可以帮助学生深化对以前所学的过基础知识的理解,提高数学能力,形成运动、变化、联系的意识,而且能较自然地培养学生辩证唯物主义的世界观。?
一、常量与变量?
辩证法认为,世界上的万事万物,都是相互联系、运动、变化和发展的。常量,是相对于某一过程或另一个变量而言的。绝对的常量是没有的。因为物质的运动是绝对的,静止是相对的,故物动则变。既然如此,相对的常量是有的,绝对的常量是不存在的。因此,在教学过程中,为帮助学生认识常量与变量这一辩证关系,不妨取如下实例。(1)匀速直线运动中,速度是常量,时间与路程均为变量;且人在实际运动的过程中。绝对的匀速运动是没有的。例如在一个学生骑车回家这一日常易见的运动过程中,也免不了加速、减速、刹车等情况。(2)电影院里统计票房收入,对某一个场次和座位类别而言,票价是常量,而售票张数和收入均为变量;但相对于某个较长时间间隔而言,由于演出的内容、种类、档次的不同,其票价仍是一个变量。(3)某日或连续几日测量某同学的身高,可以近似地看做常量;但是此同学的身高,如果从一个较长时间去看,则又是变量了。
教学实践表明,要使学生认识常量与变量这一辩证关系,就必须多形式、多角度、多层次地予以阐释。?
二、运动与静止?
根据人类认识事物的客观规律及青少年实践和知识的发展水平,我们可结合教材中的具体教学内容,引导学生逐步认识事物的绝对运动与相对静止这一辩证关系。?
例如,我们可以引导学生从教科书上看到的,在练习本或黑板上画出的y=x的图象去思考:这个图象表面上是静止的,但从列表、描点到连线的过程去看却是运动的、变化的。再进一步挖掘,可以发现:画成的图象表面上是完整的,其实是不完整的,因为它还可以向两方无限延伸,即不断运动、发展和变化,画出的函数图象永远只能是局部的,它只能是某个函数图象的一个象征物;同时这一例举也体现了部分与整体的辩证统一。?
三、内容与形式
根据现行教材体系,初一上学期,学生学习了方程的有关概念后会认为,形如y=2x+1的式子表示一个二元一次方程;初三学生刚接触一次函数概念时,会认为y=2x+1表示一个一次函数;当学生用描绘函数图象的一般方法描出y=2x+1的图象后,又认识到y=2x+1还可以表示一条直线。从哲学的角度去看,y=2x+1表示一类事物的本质联系,其内容是极其丰富的,而表达这丰富内容的形式却是相同的。这正表明,同一事物在不同的外部条件下可有多种不同的外部表现形式,相同的外部形式可以表示不同的本质内容。随着学生知识的增多和认识能力的提高,他们对事物本质的认识也将逐步地从感性上升为理性。?
四、特殊与一般?
辩证法认为,一般性寓于特殊性之中。教材中涉及特殊与一般这一内容至少有以下几个方面: (1)y=kx与y=kx+b;(2)y=ax2与y=ax2+k;(3)y=ax2与y=a(x-h)2;(4)y=ax2与y=ax2+bx+c。它们之间的关系,均是典型的特殊与一般之间的关系,而这一关系又是辩证统一的。为利于学生认识事物的本质属性,教材中总是先介绍简单的、特殊的内容,然后再逐步推广、逐步加深到较复杂的、更一般的内容,从而引导学生逐步认识事物的本质属性,掌握对事物的认识规律。?
五、现象与本质
在物质世界中,没有一定的现象,就不能表现出事物的本质,而且其本质常常寓于现象之中。当然,个别现象不一定能暴露出事物的本质,因为本质是若干同类现象的寓归。这在数学上也会如此。?
例如,在初一年级,学生可以顺利地判定方程组的解集为空集,而相对于认识"y=2x+1与y=2x+3表示两条平行直线,自然没有交点",属于对事物表象 --现象的认识;只有达到透彻理解一次函数的概念与性质以后,才算是认识了事物的本质。一元二次方程x2+2x+3=0为什么没有实数解?函数 y=x2+2x+3的图象与x轴为什么没有交点?函数y=x2+2x+3的最小值是多少?学生从"实数的偶次幂非负"到"列表--描点--连线",直观地看抛物线y=x2+2x+3的顶点的位置。到最一般地研究函数y=x2+2x+3的最小值,实乃学生由浅入深,由现象到本质的认识过程。这类问题中,方程没有实数根,或图象与x轴没有交点,或顶点在x轴上方,均是现象,而问题的本质,恰恰是"一元二次方程根的判别式"的值的状况对于这类问题的制约。再比如,研究如何去求解x-3>0, x-3=0,x-3<0,也均属于对现象的认识,而准确地认识函数y=x-3的性质,才是对事物本质的认识。
从外部形式看,y=a1x2,y=a2x2+k,y=a3(x-h)2,y=a4(x-h)2+k,y=a5x2+bx+c,它们各不相同;但当 ai(i=1,2,…,5)为非零实常数,b、c、h、k均为实常数时,它们的本质特征就暴露了出来,显现在我们眼前的竟是同一类事物:均代表一条抛物线;特别地,当a1=a2=a3=a4=a5≠0时,它们的共性就暴露得更加彻底,后四条抛物线均可由y=a1x2经适当改变位置而得到,而开口方向、大小均不改变。
六、具体与抽象
现代认知科学理论告诉我们,人类对事物本质属性的认识,是由现象到本质、由具体到抽象、由浅入深的渐进过程。感性认识常来之于对某些具体实践的思考;而理性认识则来之于对这些初步认识概括和抽象的过程,从而达到对事物本质属性的认识。因此只有从具体的感性认识上升发展为抽象的理性认识以后,才容易纳入原有的认知结构,才可以转化为运用的能力,才能为更高级的抽象提供基础和保证。我们可从细读教材中发现,无论是对正比例函数、一次函数、二次函数的研究,还是对反比例函数的图象及性质的讨论,都是从具体到抽象逐步展开论述和论证,从而加深对这些知识的理解。为了使学生的认识不局限于具体,而使之逐步上升为抽象,教材中每讲好一些具体的、典型的例题后,总是来一个"一般地,函数……具有以下性质……",从而抓住了本质联系。正是这个"一般地",构成了学生认知的困难。为了帮助学生克服认知障碍,我们应给学生以丰富的感性材料,使之产生丰富的感性认识,而后逐步上升为理性认识。
七、量变与质变
本章体现量变与质变观点的内容,例子很多,要使学生深刻认识这些内容却是很困难的,因而我们在教学时宜逐步引导,点滴渗透,而后去系统推进对这些内容的理解。(1)对于一次函数 y=kx+b,若从k≠0变为k=0,情况如何?(2)二次函数y=ax2+bx+c中,规定 a≠0;若令a=0,情况如何?(3)反比例函数y=中,自变量x的取值范围是x≠0;如果x=0,或y=0,又将如何?(4)对于y=kx+b,从k>0变为k<0,则其变化特征如何相应变化?(5)对于二次函数y=ax2+bx+c,若Δ>0变为Δ=0或Δ<0,相应的函数图象及性质将如何改变?(6)对于周长确定的矩形,当相邻边长均为周长的时,面积的大小有何特征?(7)对于一般的二次函数y=ax2+bx+c,从x<-变为x=-,再变为x>-,其增减趋势如何相应地改变??
诸如此类,均是量变积累到一定程度导致质变的例子。
八、有限与无限?
事物或数量中,有限总是表现为具体的,因而我们对这一概念可以穷极或易于理解,或能完全把握;而无限则是抽象的,它是一种运动无限延长的过程,是物的一种变化发展趋势,是一种抽象的理念,需反复渗透方可形成一定程度的认识。
(1) 学生"准确地""画出函数y=2x-1的图象",其实只是画出了这个函数图象的一个有限部分,远非全部,即用有限的部分去"表示""无限"的趋势。(2) 列表、描点、连线,画出抛物线,显然也只是画出了函数图象的一个"部分",用"有限"的一些点"确定"其"大致"位置、形状、大小,而连线是从有限走向了无限。(3)在画反比例函数的图象时,关于有限与无限、极限的思想体现得更为充分,例如观察教科书上例题y=的图象,当x(或y)的绝对值越大(或越小) 时,y(或x)的绝对值如何变化?何谓"无限接近"而"永远不能到达"两坐标轴?(4)坐标轴上有多少个点?坐标轴有多长?一个象限内有多少个点?直角坐标平面内有多少个点?坐标轴上任意两点之间有多少个点?以坐标平面内任一点P(a,b)为圆心,任意小的正数r为半径作圆,圆内有多少个点?圆上有多少个点?圆外还"剩余"多少个点?抛物线可以画多长?……?所有这些具体的、生动的材料,都在向学生对数的理解方面潜移默化地渗透着无限、极限等观点。
九、离散与连续
离散与连续是一个矛盾的两个方面,但在列表--描点--连线的过程中,连线使离散与连续得到了统一。如教科书上画y=x及y=x2的图象,均采用了由简单到复杂、从特殊到一般、由离散到连续的手法,体现了这种对立统一的关系。
仔细分析教材,不难发现《函数及其图象》这一章中,渗透和体现的上述辩证观点的内容是十分丰富的。主要观点除上面已叙述的内容之外,至少还有微观与宏观,直与曲,精确与近似,部分与整体,绝对与相对,主观与客观辩证统一等内容。限于篇幅,不再一一赘述。
为帮助学生培养辩证唯物主义的世界观,我们应根据教材中相关的教学内容,结合学生的认识水平,有目的、有计划、有系统、有重点地组织教学内容,采用学生易于接受的教育、教学方法,适当渗透,系统推进,当渗透到一定程度时,再适时进行整理,适度地进行概括和抽象;日积月累,使这些教学内容在学生的头脑中系统地并深刻地扎下根去。这样,教学大纲中规定的培养辩证唯物主义观点的任务就可以顺利完成。